 Impressum
Impressum

 Vergrößern Vergrößern
|
Die heute im Allgemeinen als Gamma bekannte Zahl wird als viertwichtigste spezielle Konstante der Mathematik hinter pi, e und i angesehen und wird für immer mit Leonard Euler verbunden sein. Auf unserer spannenenden Entdeckungsreise zu Gamma treffen wir neben historischen Zusammenhängen auf die harmonische Reihe, den Logarithmus, die Zeta-Funktion, die Gamma-Funktion, die Primzahlen und das größten ungelöste Problem - die Riemannschen Vermutung.

|
Allgemeines zum Buch
Eines gleich zu Beginn – dies ist kein polulärwissenschaftliches Buch sondern für “wirkliche” Mathematikliebhaber geschrieben. Aber wie schwierig ist die Mathematik in diesem Buch. Dazu lassen wir den Autor kurz zu Wort kommen:
“Das ist natürlich eine subjektive Frage. Ich bin nicht vor der Verwendung von Symbolen zurückgeschreckt, denn anderenfalls wäre es nur möglich gewesen, über Mathematik zu reden, anstatt sie tatsächlich zu betreiben. Dennoch verwenden wir nur wenige wirklich fortgeschrittene Techniken; vielmehr sind es zumeist einfache Ideen, die wir an einigen Stellen in fortgeschrittener Weise verwenden. In der Mathematik wird zwischen den üblicherweise synonymen Ausdrücken “elementar” und “einfach” unterschieden: “elementar” bedeutet, dass keine sehr tiefgründigen mathematischen Kenntnisse vorausgesetzt werden; mit “einfach” ist hingegen gemeint, das keine übermäßigen mathematischen Fähigkeiten erforderlich sind. In diesem Sinn ist der Inhalt des Buches häufig elementar, aber stellenweise nicht ganz einfach.”
Im fast 50-seitigen Anhang sind für alle weniger eingeweihten Leser die fortgeschrittenen Themen wie die Taylorreihen, die komplexe Funktionentheorie und die Zeta-Funktion sehr gut erklärt.
Zum Inhalt des Buches
Ein Blick ins üppige Inhaltsverzeichnis dieses Buches verrät uns, dass Gamma irgendwie mit dem Logarithmus ln und der harmonischen Reihe Hn=1+1/2+1/3+…+1/n zusammenhängt. Und tatsächlich, Euler definierte Gamma durch
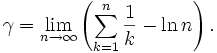
In Kapitel 4 wird die reizvolle und geheimnissvolle Zeta-Funktion
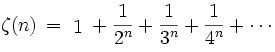
In Kapitel 6 und 7 wird die Gamma-Funktion
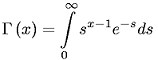
Kapitel 9 zeigt die Existenz von Gamma und fragt nach ihrem exakten Wert, kann aber in den folgenden Kapitel dennoch nur schrittweise verbessernde Approximationen liefert. Zudem ist nicht einmal bekannt, ob Gamma überhaupt irrational ist. Gamma taucht in vielen Zusammenhängen der Analysis und Zahlentheorie auf. Kapitel 12 stellt einige wenige davon vor. Analog zeigt Kapitel 13 die harmonischen Reihe aus anderen Blickwinkeln, wie zum Beispiel bei der Mittelwertbildung, in der Musik, beim Kartenmischen und beim Sortieren. Und schließlich ist Kapitel 14 für den Logarithmus und dessen Anwendung in der Mathematik und Physik reserviert.
Das vorletzte Kapitel beweist den berühmten Primzahlsatz in einer schwachen und starken Form. In der schwachen Form besagt der Satz, dass die Verteilung der Primzahlen die kleiner gleich x sind, durch x/ln(x) abgeschätzt werden kann. Die stärkere Version liefert eine genauere Approximation durch den oben erwähnte Integrallogarithmus.
Ein Teil des letzen Kapitels, in dem es um die Riemannsche Vermutung geht, fällt – wie oben schon angedeutet – nicht in die Kategorie “elementar”, denn in diesem Kapitel benötigt man Begriffe und Resultate aus der Funktionentheorie, insbesondere die komplexe Differentation und Integration. Grob gesprochen, versuchen die Mathematiker seit 1859 zu zeigen, dass die (nichttrivialen) Nullstellen der verallgemeinerten Riemannschen Zeta-Funktion alle auf einer Geraden liegen.
Ohne Einschränkungen kann dieses Buch jedem Mathematikstudenten, Wissenschaftler oder Ingenieur empfohlen werden. Wem jedoch die letzten beiden Kapitel zu anspruchsvoll sind, wird dieses Buch dennoch in den Bann ziehen, da jedes Kapitel auch unabhängig von den anderen gelesen werden kann.
Inhaltsverzeichnis